Note: Characters encodings now days seems to be narrowing down to Unicode (UTF16, UTF8, ..). There are still applications and files out there which will have a character encoding other than a member of the Unicode family, but that's generally because they are older files/formats/software. I mention character encodings here as a lead in to a future post. The following is more a of a logical flow of understanding encodings, rather than recitation of the historic development of the topic.
Let’s start at the bottom.
The data we examine, as analysts, is essentially ones and zeroes. Our data is stored, transmitted, read, and written in some form of ones and zeroes everyday. Often the data we look at is unrecoverable, lost files, fragments, deleted, and overwritten.
We may stumble upon the data of possible interest by luck, search hits, or proximity to other data of interest. It could also be something new that we haven't seen before. Since the data may lack providence or an indicator of its origins (i.e. file signature or other identifying data structure) finding out what that data is can be challenging.
If we can identify a pattern within the data that we can associate with a known pattern, we can then start to work with it. One of the ways we can initially work with data is by interpreting how the data is displayed. As a forensic analyst we are not changing the underlying data, but rather we are determining how to represent the data for display.
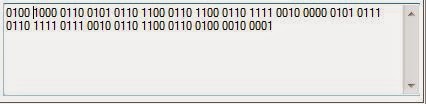
So in the bottom image is binary, a swimming sea of ones and zeroes. I find that if I stare to long at the binary it starts to stare back and I have to look away. It is a little difficult to get a purchase on.
We may stumble upon the data of possible interest by luck, search hits, or proximity to other data of interest. It could also be something new that we haven't seen before. Since the data may lack providence or an indicator of its origins (i.e. file signature or other identifying data structure) finding out what that data is can be challenging.
If we can identify a pattern within the data that we can associate with a known pattern, we can then start to work with it. One of the ways we can initially work with data is by interpreting how the data is displayed. As a forensic analyst we are not changing the underlying data, but rather we are determining how to represent the data for display.
So in the bottom image is binary, a swimming sea of ones and zeroes. I find that if I stare to long at the binary it starts to stare back and I have to look away. It is a little difficult to get a purchase on.
Since a stream of ones and
zeroes is little difficult to handle for most analysts, let’s move one step
up. We can group these ones and zeros into four bit segments. This gives us a
“nibble”. This is visually a little more pleasing. By organizing the data in a structured way I have begun to develop a place to look for patterns. I can also make out patterns without constantly losing my place.
A nibble can have a value range of 0 to 15. This range is simply a conversion of the binary (1 or 0) representation into a decimal representation. Decimal representation is something we are innately familiar with as it’s our basic enumeration scheme. I have ten fingers therefore I can count in decimal (aka base ten). The draw back to decimal representation is that a nibble ends up being presented as one to two decimal digits (i.e. 0-15). For display and pattern discovery purposes it is much easier to work with a single digit to represent a nibble. In order to avoid having a variable number of digits we use hexadecimal (aka base 16) to represent the value for each nibble. This turns the group of binary digits (1 or 0) into a single character representation i.e. for a given four binary digit segment (a nibble) I use one hexadecimal value in it's place. See the table:
Binary
|
Hexadecimal
|
Decimal
|
0000
|
0
|
0
|
0001
|
1
|
1
|
0010
|
2
|
2
|
0011
|
3
|
3
|
0100
|
4
|
4
|
0101
|
5
|
5
|
0110
|
6
|
6
|
0111
|
7
|
7
|
1000
|
8
|
8
|
1001
|
9
|
9
|
1010
|
A
|
10
|
1011
|
B
|
11
|
1100
|
C
|
12
|
1101
|
D
|
13
|
1110
|
E
|
14
|
1111
|
F
|
15
|
Using the above table you can easy convert the binary
nibbles into hexadecimal representation.
Now we have moved on from a stream of ones and zeroes, to a
stream of [0-9, A-F]. It’s only a slight improvement. The next step up is
grouping our hexadecimal nibbles into octets, or groups of eight. It's called an octet, since even though be are using hexadecimal for the representation, underneath it all it is just still 8 binary digits. So to recap, each
hexadecimal character is one nibble, so if we group two hexadecimal characters
together we have an octet.
I’m unsure of the historical reasoning, but from a logical
standpoint a single nibble is insufficient to store an alphabet letter. A
single nibble was a value range of [0-15] which can be used to represent 16
different possible states (i.e. letters). Most alphabets contain more than
sixteen letters (plus numeric digits and punctuation used in the language). By grouping nibbles
into octets we can now can represent [0-255] or 256 different characters.
Language
|
Number of letters in alphabet
|
English
|
26 letters
|
German
|
26 letters + diacritic/ligature combinations
|
French
|
26 letters + diacritic/ligature combinations
|
Spanish
|
27 letters + diacritic combinations
|
Arabic
|
28 letters
|
Source: Wikipedia
For most languages the “character set” which composes the
language can easily be represented by an octet value [0-255], the exceptions to
this will be discussed later. One octet is the same as saying one byte, as a
byte is typically considered to be eight bits. A “character set” includes punctuation,
letters (lower and upper if applicable), digits, and other characters needed to
communicate in a language.
A “character encoding” is the scheme used to translate the
binary representation of a character to a display (or printable) character
representation and vice versa.
Let’s
look at one of the first encoding schemes used for computers, ASCII, to help
clarify this concept. The ASCII encoding
is a 7-bit encoding scheme which means that it can be used to encode up to 128 (0-127) different possible characters. In the chart below the top row column is the
first nibble and the left most column represents the second nibble of an octet representing one character.
If I wanted to encode the letter ‘a’ (lower case) into the
appropriate binary digits representation I would end up with “0110 0001” which
is “61” in hexadecimal or “97” in decimal representation. To do so using the table below you would perform the following steps
1.
Locate the letter ‘a’ in
the table below.
2. Identify the binary nibble associated with the column for 'a'. In this case the column for letter is “0110”, this becomes our first nibble of the octet.
3. Identify the binary nibble associated with the row for 'a'. In this case the row for the letter is “0001” this becomes the second nibble of our octet.
4.
“0110 0001” = hexadecimal (61) = decimal
(97) = ASCII (‘a’)
0000
|
0001
|
00010
|
0011
|
0100
|
0101
|
0110
|
0111
|
|
0000
|
NUL
|
DLE
|
SP
|
0
|
@
|
P
|
`
|
p
|
0001
|
SOX
|
DC1
|
!
|
1
|
A
|
Q
|
a
|
q
|
0010
|
STX
|
DC2
|
“
|
2
|
B
|
R
|
b
|
r
|
0011
|
ETX
|
DC3
|
#
|
3
|
C
|
S
|
c
|
s
|
0100
|
EOT
|
DC4
|
$
|
4
|
D
|
T
|
d
|
t
|
0101
|
ENQ
|
NAK
|
%
|
5
|
E
|
U
|
e
|
u
|
0110
|
ACK
|
SYN
|
&
|
6
|
F
|
V
|
f
|
v
|
0111
|
BEL
|
ETB
|
^
|
7
|
G
|
W
|
g
|
w
|
1000
|
BS
|
CAN
|
‘
|
8
|
H
|
X
|
h
|
x
|
1001
|
HT
|
EM
|
(
|
9
|
I
|
Y
|
i
|
y
|
1010
|
LF
|
SUB
|
)
|
:
|
J
|
Z
|
j
|
z
|
1011
|
VT
|
ESC
|
*
|
;
|
K
|
[
|
k
|
{
|
1100
|
FF
|
FS
|
+,
|
<
|
L
|
\
|
l
|
|
|
1101
|
CR
|
GS
|
-
|
=
|
M
|
]
|
m
|
}
|
1110
|
SO
|
RS
|
.
|
>
|
N
|
^
|
n
|
~
|
1111
|
SI
|
US
|
/
|
?
|
O
|
_
|
o
|
DEL
|
Note: The
inner whites cells are printable characters and the darker cells are unprintable control
characters. Unprintable control characters include: tab, carriage return, new
line, escape, and delete. Majority of the remaining unprintable control
characters are obsolete and mostly unused for modern computing.
Binary can be a pain to work with, so to make it easier here
is the same chart with hexadecimal values instead of binary. Using the grouping
of octet values in the image found above you should be able (using the table
below) to decode the hexadecimal into a message. Note: Substitute a space character for “SP”,
a tab for “HT”, and a return for “CR”
and “LF” if encountered. These are formatting characters and are considered unprintable in the terms of display.
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
0
|
NUL
|
DLE
|
SP
|
0
|
@
|
P
|
`
|
p
|
1
|
SOX
|
DC1
|
!
|
1
|
A
|
Q
|
a
|
q
|
2
|
STX
|
DC2
|
“
|
2
|
B
|
R
|
b
|
r
|
3
|
ETX
|
DC3
|
#
|
3
|
C
|
S
|
c
|
s
|
4
|
EOT
|
DC4
|
$
|
4
|
D
|
T
|
d
|
t
|
5
|
ENQ
|
NAK
|
%
|
5
|
E
|
U
|
e
|
u
|
6
|
ACK
|
SYN
|
&
|
6
|
F
|
V
|
f
|
v
|
7
|
BEL
|
ETB
|
^
|
7
|
G
|
W
|
g
|
w
|
8
|
BS
|
CAN
|
‘
|
8
|
H
|
X
|
h
|
x
|
9
|
HT
|
EM
|
(
|
9
|
I
|
Y
|
i
|
y
|
A
|
LF
|
SUB
|
)
|
:
|
J
|
Z
|
j
|
z
|
B
|
VT
|
ESC
|
*
|
;
|
K
|
[
|
k
|
{
|
C
|
FF
|
FS
|
+
|
<
|
L
|
\
|
l
|
|
|
D
|
CR
|
GS
|
-
|
=
|
M
|
]
|
m
|
}
|
E
|
SO
|
RS
|
.
|
>
|
N
|
^
|
n
|
~
|
F
|
SI
|
US
|
/
|
?
|
O
|
_
|
o
|
DEL
|
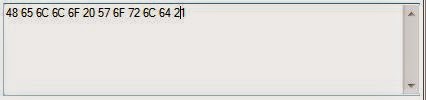
If you ended up with the following message, then your decoding of
the hexadecimal was successful.
You now have the necessary tools to start identifying text based on ASCII from a raw hexadecimal representation. Here are a few additional rules to help you.
- Average word length - Within English the approximate average word length is 5 characters.
- Average sentence length - A sentence is approximately 4 - 8 words in length.
- Sentence Termination - Sentences are typically terminated by punctuation.
- Word Spacing - Words are separated by spaces within the sentence.
- Word grouping - Sentences are grouped into paragraphs.
- Upper/lower case frequency - Typically, words only start with a capital letter if it is a proper noun or at the beginning of a sentence.
- Look for letters - Values on average range between 0x21 to 0xE7 (33 to 231 in decimal). This is the printable character ranges in ASCII for the English language. If you are working in a language other than English your range is of course different, and often is larger. See the ASCII chart; this range makes the first printable character "!" and the last "~".
- Look for a high frequency of letters: The frequency of character occurrence will be higher in the 0x41-0x5A ("a-z") and 0x61-7A ("A-Z") ranges. These character occur more frequently in a sentence.
- Sentence termination - Sentences terminate in a period, exclamation point, or question mark (0x21, 0x2E, 0x3F).
- Word spacing - Hexadecimal groupings are separated by 0x20 (space).
- Word grouping - Paragraphs terminate in a line feed, or carriage return, or both. These are formatting characters which indicate the end of a paragraph. These are identified on the ASCII chart as 0x0A (LF) and 0x0D(CR). Depending on operating system, programmer, or other factors you may see 0x0D0x0A (CRLF) or just the single CR/LF by itself.
- Upper/lower case frequency - Expect to see more hex in the range 0x61-0x7A (lower case), over the range 0x41-0x5A(upper case).
Where does it start?
Where does it end?
The first thing I tend to notice is the spaces "0x20". Knowing the alphabet ranges of 0x41-0x5A (upper case) and 0x61-0x7A(lower case) I can start selecting narrowing down my area of interest.
Times up, see the picture below to see if you were in proximity to the answer.
Let do a quick review of my approach:
- Look for spaces (0x20). Should have an average number of hex octets between spaces of 5 to 8.
- Locate the start. My first line that I really feel strong with is the 7th line from the bottom (address 0x7D2) that begins with the hex "75 20 6E". The two characters that proceed that line are still within my valid range.
In the real world your forensic tool usually does the work for you, but this was to give you a structured approach in your analysis and to prepare you for the up coming data visualization posts.
Let's finish with the topic on ASCII with how it relates to 8bit encodings that support ASCII and an additional alphabet.
The ASCII encoding forms the basis of a large number of other 8 bit character encoding schemes. Keep in mind that the ASCII encoding is originally 7 bits ... which can represent 128 different characters. A byte (which is 2 nibbles or 1 octet) can be used to represent 256 different values. This means that if a byte is used to store a character, that there is an additional 128 values being unused. Have a look at the image below. The image is gridded into 256 cells. The first 128 cells are the ASCII encoded values (in green) with the remaining area in red being unused by the ASCII encoding.
Image: ASCII
The ASCII encoding works fine for the English speaking world, and other written languages whose alphabet does not stray from the English alphabet. However for languages with partial alphabet overlap (i.e. has diacriticals, or punctuation, and other characters), such as Western\Eastern European languages et al, then ASCII is not sufficient to the task. However, the unused encoding space not occupied by ASCII can be used to represent these other characters. The top half (in red) of the encoding space is utilized by various 8 bit encodings to extend ASCII. Examples of a few of these encodings can be seen below. Note: I fought with the wording of top half vs bottom half. The extension to ASCII is in the bottom of the grid, but occupies a higher hex value range .. so I settled on using top half. Sorry for the confusion.
Image:Latin 9 AKA ISO-8859-15
Image:Cyrillic AKA ISO-8859-5
Image:Arabic AKA ISO-8859-6
Image: Hebrew AKA ISO-8859-8
Note: I generated the above images by have a program run through the 256 possible binary values and draw out the associated character for a given Encoding. Repeating the process for each of the character encodings above. It looks like in my haste I chose a Font which didn't support the whole character set for two of the encodings. This however gives me a teaching moment, so win - Typically software will display a square or symbol with a question mark when it can't render a character using the selected font.
The short of it is :
Note: I generated the above images by have a program run through the 256 possible binary values and draw out the associated character for a given Encoding. Repeating the process for each of the character encodings above. It looks like in my haste I chose a Font which didn't support the whole character set for two of the encodings. This however gives me a teaching moment, so win - Typically software will display a square or symbol with a question mark when it can't render a character using the selected font.
The short of it is :
- A large number of 8 bit character encoding schemes are based on ASCII and share the ASCII character space.
- From the stand point of forensic tools we are choosing an encoding as means to interpret/represent the stored data for display.
- Look for patterns in your data.
to be continued ...
Edit: put the wrong word in the title, fixed it.
Edit: put the wrong word in the title, fixed it.












No comments:
Post a Comment